경기도미래기술학교 AI개발자 부트캠프 34일차 TIL- KNN 알고리즘 1탄.

#결정계수 구하는 식 : 타겟 - 예측 제곱의 합 / 타겟 - 평균 제곱의 합

 

결국 문제 해설은 하지 않았고... 슥 훑고 넘어갔다. 나중에 시간 써야 하는 부분이다.

그래도 어제 복습한 내용들 대충은 있으니 그것들 참고해서 진행하자.

 

k-Nearest Neighbor

 

KNN은 전에 동빈나 강의를 사알짝 봤었다.

 

https://www.youtube.com/watch?v=QRWNto6BsfY 

 

그래서 예제 표로 두 점 사이의 거리를 구하는 식을 연습했다.

# 5 : speed = 2.75, agility = 7.50
# 12 : speed = 5.00, agility = 2.50

# 유클리디언 : √((5.00 - 2.75)² + (2.50 - 7.50)²)
def euclidean_distance(x1, y1, x2, y2):
    result = (((y1-x1)**2) + ((y2-x2)**2)) ** 0.5
    return result

#맨하탄 : |x2 - x1| + |y2 - y1|
def manhattan_distance(x1, y1, x2, y2):
    result = abs(y1 - x1) + abs(y2 - x2)
    return result


id_5_speed = 2.75
id_12_speed = 5.00

id_5_agility = 7.50
id_12_agility = 2.50
print('5 to 12')
print('euclidean_distance: ', round(euclidean_distance(id_5_speed,id_12_speed,id_5_agility,id_12_agility),2))
print('manhattan_distance : ', manhattan_distance(id_5_speed,id_12_speed,id_5_agility,id_12_agility))

id_17_speed = 5.25
id_17_agility = 9.50

print('12 to 17')
print('euclidean_distance: ', round(euclidean_distance(id_12_speed,id_17_speed,id_12_agility,id_17_agility),2))
print('manhattan_distance: ', manhattan_distance(id_12_speed,id_17_speed,id_12_agility,id_17_agility))

 

두 개의 차이가

 

5 to 12
euclidean_distance:  5.48
manhattan_distance :  7.25
12 to 17
euclidean_distance:  7.0
manhattan_distance:  7.25

유클리디언 거리는 직선거리여서 값이 다르게 나왔는데

맨하탄 거리에서는 수직, 수평 직선대로 가기 때문에 같은 값이 나왔다.

 

 

KNN 알고리즘에서 k의 값은 홀수로 들어가야 한다.

 

디시전 바운더리 : 타겟값이 달라지는 경계

 

np.random.normal을 사용한다.

 

np.random.uniform : 표준정규분포(low=0.0, high=1.0, size=None)

 

np.random.randint

 

np.random.randn : size만 들어간다. 마찬가지로 표준정규분포이다.

의 차이를 꼭 알자. 자주 쓰니까.

 

import numpy as np
import matplotlib.pyplot as plt

# np.random.uniform(low, high, size)
# np.random.randint(low, high, size)
# np.random.randn(size)

# 하이퍼파라미터 초기화

n_data = 100
x_data = np.random.normal(loc=5, scale=5, size=(n_data, ))

#그래프 그리는 그래프 객체 ax를 생성한다.
fig, ax = plt.subplots(figsize=(5, 5))
#rwidth=0.7는 막대기 두께임.
ax.hist(x_data, rwidth=0.7)
plt.show()

np.random.seed로 값을 고정해서 확인할 수 있다.

 

import numpy as np
import matplotlib.pyplot as plt

#np.random.normal로 random data를 만들고, ax.hist를 이용해 히스토그램 만들기.

#loc : 평균, scale : 표준편차. #size: 추출할 숫자 갯수
n_data = 100
x_data = np.random.normal(loc=5, scale=5, size=(n_data,))


# 2. 평균이 (5,3)이고 표준편차가 x, y 방향으로 모두 1인 (100, 2) dataset 만들기

np.random.seed(50)  # 시드 설정

x_data = np.random.normal(loc=(5, 3), scale=(1, 1), size=(100, 2))

print(x_data)
print(x_data.shape)

print('mean : ', x_data.mean(axis=0))
print('std : ', x_data.std(axis=0))

# fig, ax = plt.subplots(figsize=(20, 15))
# ax.hist(x_data, rwidth=0.8)
# plt.show()

#최솟값, 최댓값, 추출할 숫자 갯수
uniform_dataset_test = np.random.uniform(low=5,high=20, size=30)

print(uniform_dataset_test)

n_data = 100
x_data = np.random.normal(loc=5, scale=1, size=(n_data,))
y_data = np.random.normal(loc=3, scale=1, size=(n_data,))

print(x_data.shape,y_data.shape)

x_data = x_data.reshape(-1,1)
print(x_data.shape)

y_data = y_data.reshape(-1,1)
print(y_data.shape)

data_ = np.concatenate((x_data,y_data),axis=1)

print(data_.shape)

print(data_.mean(axis=0))
print(data_.std(axis=0))

강사님의 방법. reshape를 다시 보기, concatenate 다시 해보기. 다른 방법 없는지? 찾아보기.

 

a = []
b = np.array([])
print(type(a),type(b))

print('----list-----')
for attr in dir(a):
    if not attr.startswith('_'):
        print(attr)

print('----numpy-----')
for attr in dir(b):
    if not attr.startswith('_'):
        print(attr)

넘파이를 리스트보다 많이 사용하는 이유. 기능들이 훨씬 많다~

 

import random

import numpy as np
import matplotlib.pyplot as plt

#무게중심을 random하게 만들고 dataset의 모양이 (100,2)가 되도록 만들기.
#scatter plot으로 시각화하기.

test_random_x = random.randint(10,20)
test_random_y = random.randint(10,20)
print('test_random_x:',test_random_x)
print('test_random_y:',test_random_y)
x_data = np.random.normal(loc=(test_random_x, test_random_y), scale=(1,1), size=(100, 2))

print(x_data.shape)

centroid = np.mean(x_data, axis=0)

print('centroid: ', centroid)
plt.figure(figsize=(8, 8))
plt.scatter(centroid[0], centroid[1], color='red', s=50)
plt.scatter(x_data[:, 0], x_data[:, 1])
plt.show()

내 방식. slice 공부를 좀 더 해야 한다.

 

centroid = np.random.uniform(low=-5, high=5, size=(2,))

n_data = 100
data = np.random.normal(loc=centroid, scale=1, size=(n_data,2))

fig, ax = plt.subplots(figsize=(5,5))
ax.scatter(centroid[0],centroid[1], c='red')
ax.scatter(data[:, 0], data[:, 1])
plt.show()

강사님 방식. 비슷한 것 같기도 하고 그렇다.

 

 

 

#4 class, class마다 100개의 점을 가지는 dataset 만들기.
#(400,2)
# class들의 centroid는 랜덤하게.

# import numpy as np
# import matplotlib.pyplot as plt
#
# np.random.seed(42)

test_random_x1 = np.random.randint(10, 20)
test_random_y1 = np.random.randint(50, 60)
test_random_x2 = np.random.randint(10, 50)
test_random_y2 = np.random.randint(25, 30)
test_random_x3 = np.random.randint(30, 35)
test_random_y3 = np.random.randint(40, 43)
test_random_x4 = np.random.randint(50, 60)
test_random_y4 = np.random.randint(50, 60)

print('test_random_x1:', test_random_x1)
print('test_random_y1:', test_random_y1)

x_data1 = np.random.normal(loc=(test_random_x1, test_random_y1), scale=(1, 1), size=(100, 2))
x_data2 = np.random.normal(loc=(test_random_x2, test_random_y2), scale=(1, 1), size=(100, 2))
x_data3 = np.random.normal(loc=(test_random_x3, test_random_y3), scale=(1, 1), size=(100, 2))
x_data4 = np.random.normal(loc=(test_random_x4, test_random_y4), scale=(1, 1), size=(100, 2))

for i in range(4):
    x_data1 = np.random.normal(loc=(test_random_x1, test_random_y1), scale=(1, 1), size=(100, 2))

x_data = np.concatenate((x_data1, x_data2, x_data3, x_data4), axis=0)

print(x_data.shape)

plt.figure(figsize=(8, 8))
colors = ['red', 'blue', 'green', 'black']
data_sets = [x_data1, x_data2, x_data3, x_data4]

for i, (data, color) in enumerate(zip(data_sets, colors)):
    start_idx = i * 100
    end_idx = (i + 1) * 100
    centroid = np.mean(data, axis=0)
    plt.scatter(x_data[start_idx:end_idx, 0], x_data[start_idx:end_idx, 1], c=color)
    plt.scatter(centroid[0], centroid[1], c='orange', marker='*')

plt.show()

 

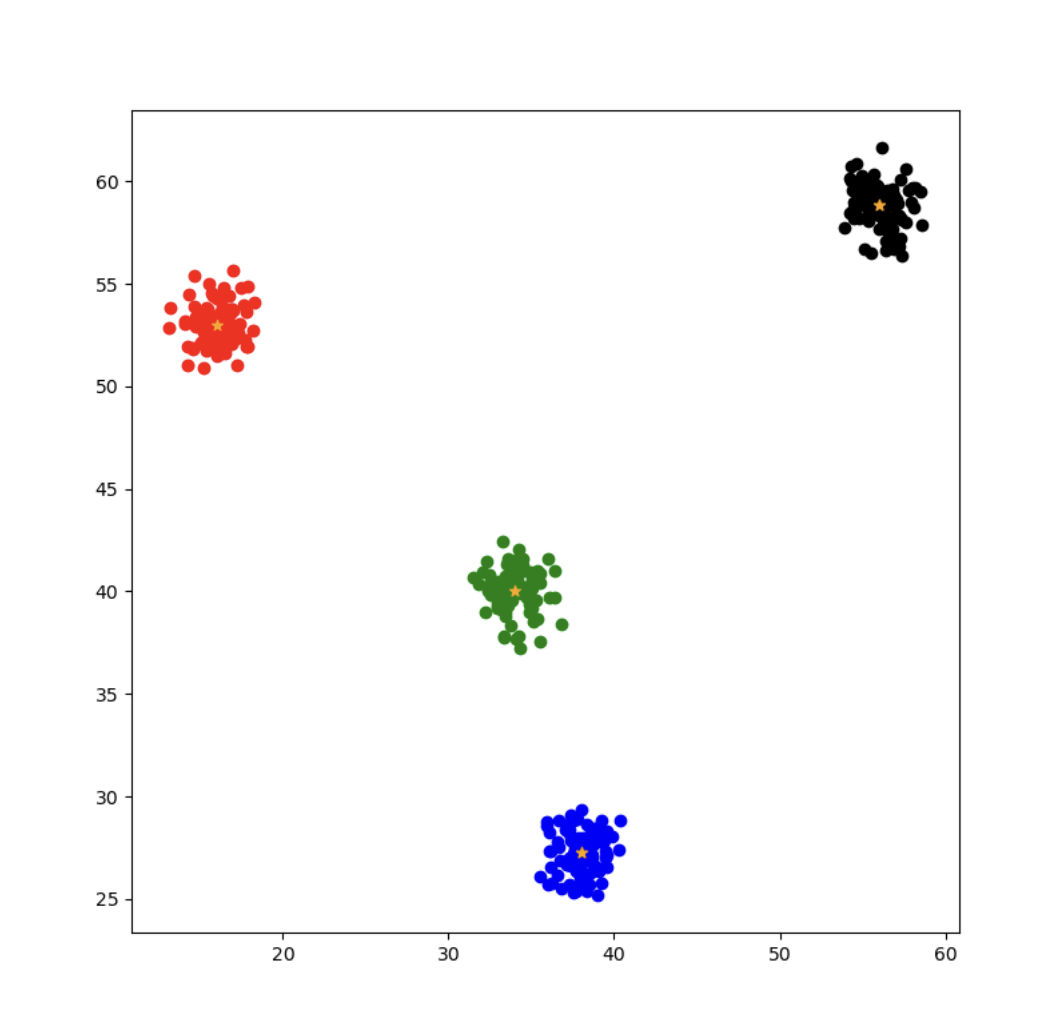
이건 내방식. 자꾸 for문으로 다시 하라는 주문을 받았다..

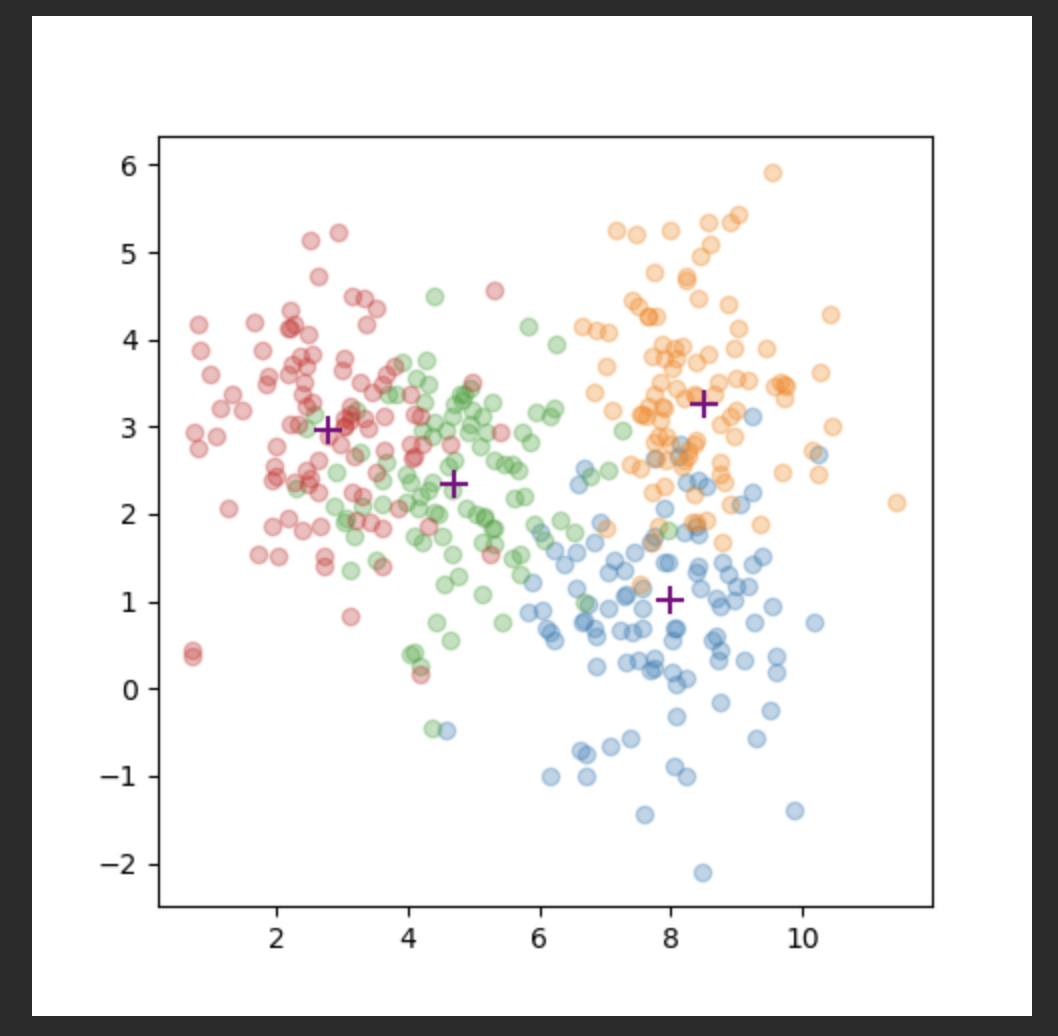
n_classes = 4
n_data = 100

data = []
centroids = []

for _ in range(n_classes):
    centroid = np.random.uniform(low=-10, high=10, size=(2,))
    data_ = np.random.normal(loc=centroid, scale=1, size=(n_data, 2))

    centroids.append(centroid)
    data.append(data_)


print(len(data), len(centroids))

centroids = np.vstack(centroids)

data = np.vstack(data)
print(data.shape)

fig, ax = plt.subplots(figsize=(5, 5))

for class_idx in range(n_classes):
    data_ = data[class_idx * n_data : (class_idx + 1)* n_data]
    ax.scatter(data_[:, 0], data_[:, 1], alpha=0.3)

for centroid in centroids:
    ax.scatter(centroid[0], centroid[1], c='purple', marker='+', s=100)

plt.show()

 

강사님 방식. vstack은 버티컬 방향으로 레이어가 합쳐진다. concat이랑 비슷하다.